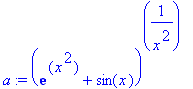
В ядро Maple входит большое количество функций, относящихся к математическому анализу. Мы рассмотрим ряд примеров, иллюстрирующих вычисление пределов, дифференцирование, интегрирование, суммирование числовых рядов, разложение функций в степенные ряды и решение дифференциальных уравнений с помощью Maple.
Для нахождения пределов служит функция limit , которая может иметь два или три аргумента. Первый аргумент. - это функция (последовательность), предел которой надлежит искать. Второй указывает переменную и значение, к которому ее надо устремить.
Смысл третьего, необязательного
параметра будет ясен из рассматриваемых
ниже примеров.
> limit(sin(3*x)/x, x=0);
3
> limit((1+1/n)^n,n=infinity);
e
> limit((exp(x^2)+sin(x)^2)^(1/(x^2)),x=0);
e2
В следующем примере предел значений
функции при стремлении аргумента к 0 не
определен, поскольку односторонние
пределы различны:
> a:= (exp(x^2)+sin(x))^(1/(x^2));
>
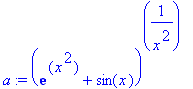
> limit(a, x=0); limit(a, x=0, left); limit(a, x=0, right);
undefined
0
![]()
В зависимости от того, где - в
действительной или в комплексной области -
ведутся вычисления, Maple по-разному
интерпретирует константу infinity (бесконечность),
различая понятия + ![]() и -
и - ![]() в области вещественных чисел или оперируя
понятием бесконечно-удаленной точки
комплексной плоскости:
в области вещественных чисел или оперируя
понятием бесконечно-удаленной точки
комплексной плоскости:
> limit(1/x,x=0, real);
undefined
> limit(1/x,x=0, complex);
infinity
Многие функции, в том числе большинство команд (функций) математического анализа, можно вызывать в так называемой инертной форме. Инертная форма функции (если она имеется) именуется так же, как и активная, с той разницей, что первая буква имени заменяется на соответствующую заглавную. (Заметим, что существуют функции, не имеющие инертной формы, имена которых начинаются, тем не менее, с заглавных букв.) В случае использования инертной формы вычисления откладываются. Этот эффект можно, в частности, использовать для оформления математических документов:
> Limit((n^3+3*n)/2^n, n=infinity) = limit((n^3+3*n)/2^n, n=infinity);
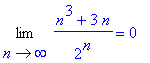
Для вычисления обычных и частных производных в Maple
используется команда (функция) diff, первый аргумент которой есть дифференцируемая функция, а второй - переменная, по которой надо брать производную.
> diff(sqrt(x^2+3), x);
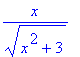
> diff(diff(z*sin(z), z), z); diff(z*sin(z), z, z);
2 cos(z) - z sin(z)
2 cos(z) - z sin(z)
Обратите внимание на эквивалентность
двух последних команд.
Еще несколько примеров:
> Diff(exp(x^2)*sin(1/x),x,x);
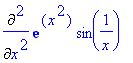
> diff(x^3+t*x+t, x);
3 x2 + t
> diff(x^3+t*x+1, t);
x
Разумеется, переменная, по которой ведется дифференцирование, должна быть именно переменной (в математическом смысле). В противном случае Maple выдаст сообщение об ошибке.
> x:=4: diff(x^2+3*x, x);
Error, wrong number (or type) of parameters in function diff
> x:='x': diff(x^2+3*x, x);
2 x + 3
>
Обратите внимание на то, как было
отменено присваивание переменной x
конкретного числового значения.
Для нахождения производной неявной функции используется
implicitdiff, у которой второй параметр - неявно заданная функция, а третий - аргумент, по которому ведется дифференцирование:
> implicitdiff(x^2+3*y*x+y^3,y,x);
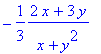
Кроме команды diff, в Maple имеется также
оператор дифференцирования D.
Проиллюстрируем его действие на примерах:
> D(x^3); D([sin,cos,tan]);
3 D(x) x2
[cos, -sin, 1 + tan2]
Вышеприведенные примеры показывают, что,
в отличие от функции diff, D не требует
второго аргумента. Дифференцируя выражение
x3, D рассматривает x не как
независимый аргумент, а как некоторую
функцию. Если результат операции
дифференцирования затруднительно записать
без использования аргумента
дифференцируемой функции, то Maple "выкрутится"
следующим образом:
> D(D(log));
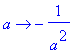
Для нахождения определенных и неопределенных интегралов в Maple используется функция int, зависящая от двух аргументов, первый из которых представляет собой подынтегральное выражение, а второй - переменную, по которой ведется интегрирование. Если для второй переменной указан диапазон изменения переменной, то Maple ищет определенный интеграл, а в противном случае - неопределенный (возращается одна из первообразных).
> int(sin(x)*x^2, x);
-x2 cos(x) + 2 cos(x) + 2 x sin(x)
> Int(x/(x^2+x+1),x)=int(x/(x^2+x+1),x);
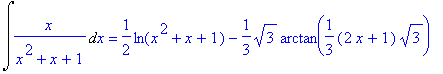
> int(x^3-t*x^2+4*t, x=1..4);
![]()
> int(sin(x)/x, x);
Si(x)
Последний интеграл не выражается
конечным числом элементарных функций. В
таких случаях Maple пытается найти интеграл,
используя специальные функции. В
приведенном примере это несложно сделать с
помощью интегрального синуса. Если же Maple
все-таки не сможет взять интеграл в
конечном числе элементарных и специальных
функций (это не обязательно означает, что он
не берется), то результатом вызова функции int
будет перевод всей команды в
математический формат так, как если бы мы
использовали инертную форму функции
интегрирования ( Int ).
> g:= int(sin(1/cos(x)), x);
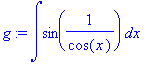
> diff(g, x);
![]()
Для численного интегрирования команда int
используется в комбинации с функцией evalf
. Причем в этом случае неважно, какая форма
функции Int используется: активная или
инертная.
> evalf(int(sin(x^2), x=1..2)); evalf(Int(cos(x^2), x=1..2));
.4945081882
-.4430627755
Maple умеет находить конечные и бесконечные
суммы, а также разлагать функции в
степенной ряд в окрестности указанной
точки и с указанной точностью. Рассмотрим
примеры:
> sum(i^3, i=0..5);
225
Во избежание ошибок (связанных, например, с тем, что переменная по которой ведется суммирования уже имела какое-то значение) рекомендуется заключать общий член и переменную суммирования в одинарные кавычки.
> sum('a[k]*x^k','k'=0..n);
![sum(a[k]*x^k,k = 0.. n)](images/mapletut130.gif)
> sum('1/k!', 'k'=0..infinity);
e
> sum('1/k^2', 'k'=1..infinity);
![]()
Как и в случае с интегралами, если ответ
не выражается в конечном числе
элементарных функций, Maple использует
специальные функции, а если и это не
помогает просуммировать ряд,
ограничивается переводом выражения в
математический формат вывода.
> sum('(1/k!)^2', 'k'=0..infinity);
BesselI(0, 2)
> sum('1/k^3', 'k'=1..infinity);
![]()
> sum('1/(k^2)!', 'k'=0..infinity);
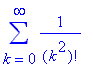
Для разложения функции в ряд Тейлора в Maple используется команда series. Она зависит от трех параметров: первый - разлагаемая функция; второй задает точку, в окрестности которой ведется разложение; третий определяет порядок бесконечно малых, с точностью до которых члены ряда будут вычисляться явно.
> f:=int(sin(x)/x, x); series(f, x=0,10);
f := Si(x)
![]()
> h:=series(log(x), x=1, 5);
![]()
Часто бывает полезно преобразовать ряд в полином, отбросив остаточный член.
> convert(h,polynom);
![]()
Дополнительные возможности манипулирования с формальными степенными рядами (например, умножения рядов) можно получить, подгрузив специализтрованный пакет powerseries.
Maple содержит специализированные пакеты DEtools
и PDEtools для решения и графического
представления решений дифференциальных
уравнений (обыкновенных и в частных
производных соответственно). Однако многие
дифференциальные уравнения можно решать, и
не подгружая этот пакет, используя функции dsolve
и pdesolve, входящие в ядро Maple:
> ode := diff(y(x),x)-y(x)^2+y(x)*sin(x)-cos(x);
![]()
> ans := dsolve(ode);
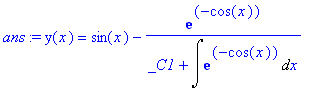
> pdesolve( diff(f(x,y),x,x)+5*diff(f(x,y),x,y)=3, f(x,y) );
![]()
C помощью Maple можно искать и частные
решения дифференциальных уравнений,
определяемые начальными условиями.
> dsolve({diff(y(x),x,x)=-2*y(x), y(0)=1, y(Pi)=1}, y(x));
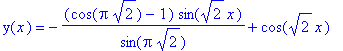
> dsolve({diff(y(x),x,x)=y(x)+exp(x), y(0)=1, D(y)(0)=1}, y(x));
![]()
![]()
Волгоградский
государственный педагогический
университет
Кафедра алгебры, геометрии и информатики