Простейшие преобразования и вычисления

 назад содержание вперед

Будучи системой символьных вычислений, Maple должен иметь средства для преобразования алгебраических выражений: приведения подобных членов (это делается по умолчанию), раскрытия скобок (expand), группировки (collect), разложения на множители (factor для многочленов и ifactor для целых чисел) упрощения выражений (simplify) и т.д. Действие перечисленных выше функций станет понятно из следующих примеров:

> collect(x^2+2*x*y-5*y-y^2+x*y^2+3,y);

(-1 + x) y² + (-5 + 2 x) y + x² + 3

> expand((x^2+x-1)*(x^2+3));

x⁴ + 2 x² + x³ + 3 x - 3

> expand(cos(3*x));

4 cos(x)³ - 3 cos(x)

> factor(a^3-b^3);

(a - b) (a² + a b + b²)

> ifactor(22!+1);

(23) (521) (93799610095769647)

> a:=sin(u)^2+cos(u)^2; simplify(a);

a := sin(u)² + cos(u)²

1

Решение уравнений, неравенств и систем

 назад содержание вперед

Для решения уравнений, систем уравнений и неравенств в Maple используется команда (функция) solve. Приведем примеры:

 > solve(x^2-3*x+2);

1, 2

Обратите внимание: если первый (а в нашем случае и единственный) аргумент solve не является уравнением (или неравенством), то Maple трактует его так, как если бы это выражение было приравнено к 0.

> solve(x^2-3*x+2<0);

RealRange(Open(1), Open(2))

> solve(x^2-3*x+2>=0);

Обратите внимание, что открытый интервал (или луч) задается в Maple с помощью функции Open, применяемой к концам интервала, задаваемого функцией RealRange. Не забудьте, что Maple чувствителен к регистру: команда open (с маленькой буквы) служит для открытия файлов.

Рассмотрим примеры решения алгебраических уравнений степеней выше второй:

> solve(x^3-2);

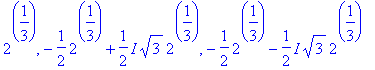
> solve(x^12=1);

Если же корни уравнения не выражаются в радикалах или их выражение слишком громоздко, Maple представляет ответ, используя функцию RootOf :

> a:=solve(x^5-3*x+7);

a := RootOf(_Z⁵ - 3 _Z + 7)

> b:=a^5-3*a;

> simplify(b);

-7

 В случае, когда корни выражаются в радикалах (например, при решении алгебраических уравнений 4-й степени) получить явное выражение корней можно, присвоив зарезервированной переменной _EnvExplicit значение true. (Альтернативные вариант: использовать функцию convert с параметром radical.)

 С помощью команды solve можно решать не только алгебраические уравнения и неравенства:

> solve(cos(x)-sin(2*x));

 При решении тригонометрического уравнения Maple привел в решения, лежащие в пределах одного промежутка периодичности (в нашем случае это интервал от - до ). Проиллюстрируем, как с помощью зарезервированной переменной окружения _EnvAllSolutions можно обеспечить вывод всех решений:

> _EnvAllSolutions := true:

> solve(cos(x)-sin(2*x));

Приведем ряд примеров применения функции solve для решения уравнений с несколькими переменными:

> solve(x^2*y+y-1);

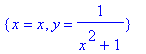
> solve(x^2*y+y-1, x);

> solve(x^2*y+y-1,y);

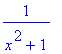
Видно, что форма вывода ответа к одному и тому же уравнению определяется вторым параметром (или его отсутствием) команды solve , указывающим, относительно какой переменной решать уравнение.

Приведем примеры решения систем уравнений:

> solve({x+2*y=5, x^2-y^2=8});

> solve({2*x+y=alpha, x-y-2=0},{x,y});

Кроме команды solve в Maple имеется целое семейство ее аналогов для решения уравнений специального вида: dsolve и pdesolve используются для решения дифференциальных уравнений; isolve - для решения уравнений в целых числах; msolve - для решения сравнений по модулю; rsolve - для явного нахождения формулы общего члена рекуррентно заданных последовательностей; fsolve - для численного решения уравнений.

 назад содержание вперед

Волгоградский государственный педагогический университет
Кафедра алгебры, геометрии и информатики