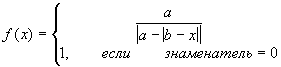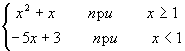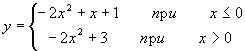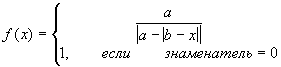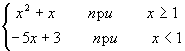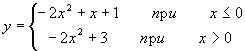Задание 1

1. Составить программу для вычисления функции:    
   
2. Найти max (a, b).
3. Дана точка М(x, y). Присвоить z = 1, если точка внутри эллипса 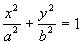   и z = 0, если точка вне эллипса.
4. Вычислить y(x), если y = x² при x > 1 и y = x при x <= 1.
5. Вычислить:
   
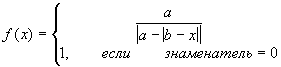
6. Даны два отрезка [a, b], [c, d] на прямой. Установить, имеют ли они общие точки или нет.
7. Дана точка М(x, y). Присвоить z = 1, если точка принадлежит окружности с радиусом R и центром в точке (a, b) и z = 0 в противном случае.
8. Вычислить функцию f(x), если f(x) = e^-x при х >= 0 и f(x) = cos x при х < 0.
9. Составить программу для вычисления y = t² - t -1, где t =
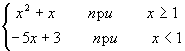
10. Составить программу решения уравнения .
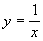11. Составить программу вычисления модуля |5x - 4|.
12. Составить программу вычисления функции:
    
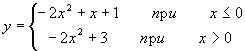
13. Составить программу вычисления корня .
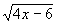14. Составить программу вычисления функции y=lg(3x-6).
15. Напечатать координаты той из точек М₁(a, b) и М₂(c, d), которая расположена ближе к началу координат.

Задание 2

1. Даны уравнения прямых а₁х+b₁y=c₁, a₂x+b₂y=c₂, a₃x+b₃y=c₃. Выяснить, какие из этих прямых параллельны и указать, если таковых не имеется.
2. В какой четверти координатной плоскости находится точка с координатами x, y (xy<>0).
3. Если сумма двух различных чисел меньше единицы, то наименьшее заменить полусуммой, в противном случае меньшее заменить суммой.
4. Даны различные действительные числа x, y, z, d. Найти max(max(x, y), max(x, z), max(z, d)).
5. Даны три действительных числа. Определить, что больше, сумма или произведение этих чисел. Если сумма больше произведения на число меньшее единицы, то вывести 0, и противном случае вывести 1.
6. Найти значение z, если
   
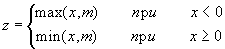
7. Даны отрезки [a, b] и [c, d] и точка A с координатой х. Определить, принадлежит ли данная точка одному из этих отрезков, обоим или лежит вне их.
8. Даны два действительных числа x и y. Если наименьшее из них отрицательно, то заменить его нулем, в противном случае единицей.
9. Определить, существует ли треугольник со сторонами a, b, c, и если существует, то является ли он равносторонним, равнобедренным или разносторонним.
10. Даны действительные числа х₁, х₂, х₃, y₁, y₂, y₃. Принадлежит ли начало координат треугольнику с вершинами (x₁, y₁), (x₂, y₂), (x₃, y₃)?
11. Даны действительные числа x, y. Если x и y отрицательные, то х присвоить модуль х. Если отрицательное одно из них, то увеличить у на 0.5. Если оба числа отрицательные, то увеличить х в 10 раз.
12. Даны три действительных числа х, у, z и отрезок [a, b]. Заменить на нули те из них, которые принадлежат отрезку и на единицы - остальные.
13. Даны различные действительные числа a, b, c, d. Найти max (max(a, b), max(a, c), max(a, d)).
14. Известно, что из четырех чисел a₁, a₂, a₃, a₄ одно отлично от трех других, равных между собой. Присвоить номер этого числа переменной n.
15. Даны уравнения прямых а₁х+b₁y=c₁, a₂x+b₂y=c₂, a₃x+b₃y=c₃. Выяснить, какие из этих прямых перпендикулярны или указать, если таковых не имеется.

Задание 3

1. Составить программу определения минимального элемента из трех элементов х₁, х₂, х₃.
2. Решить биквадратное уравнение.
3. Даны три числа a, b, c, удовлетворяющие аксиомам треугольника. Если треугольник равносторонний , то найти его площадь. Если треугольник равнобедренный, то найти периметр и угол между равными сторонами.
4. Даны два числа. Если они не равны, то найти их сумму и произведение. Если произведение больше суммы, то определить на сколько.
5. Определить направление ветвей параболы y=ax²+by+c. Найти точки пересечения параболы с осью OX.
6. Даны три числа. Определить, существует ли треугольник со сторонами длиной a, b, c и, если существует, то найти его периметр и площадь.
7. Вывести сообщение о количестве корней квадратного уравнения и найти эти корни.
8. Если w <> 0 и, при этом, w < 0.5, то поменять знак w, а если w = 0, присвоить w единицу.
9. Найти значение х и у при заданных значениях a и b:
   ,
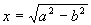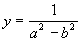
10. Определить параллельны ли прямые, заданные уравнениями у=k₁x+b₁ и y=k₂x+b₂. Если они параллельны, то найти координаты точек пересечения с осью ОХ (k₁, k₂ <> 0).
11. Дана точка М(х, у). Проверить, принадлежит ли точка окружности единичного радиуса. Если принадлежит, то уменьшить координату х на единицу, а у увеличить на значение х.
12. Даны две прямые, заданные уравнениями у=k₁x+b₁ и y=k₂x+b₂. Если эти прямые параллельны, то определить расстояние между ними.
13. Даны прямая и окружность, заданные уравнениями у=kх+b и (х-а)²+(у-b)²=r². Определить, сколько точек пересечения имеют прямая и окружность и найти координаты этих точек.
14. Даны два действительных числа а и b. Сравнить их целые части, и если они равны, то поменять местами их дробные части, в противном случае округлить эти числа.
15. Даны две окружности заданные уравнениями (х-а₁)²+(у-b₁)²=r₁² и (х-а₂)²+(у-b₂)²=r₂². Определить количество точек пересечения и найти их координаты.

назад содержание вперед

Волгоградский государственный педагогический университет
Кафедра алгебры, геометрии и информатики
Апрель 2008