Подпрограммы
назад содержание
вперед
Задание 1 (функции).
- Даны действительные числа a, b, c.
Получить:
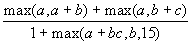
- Даны действительные числа a, b.
Получить u = min(a, b-a), y = min(ab, a+b),
k = min(u+v2, 3.14).
- Даны натуральные числа a, b, c.
Определить функцию bin(x), переводящую
число х из десятичной системы
счисления в двоичную. Найти bin(a + b), bin(ab
+ c).
- Даны действительные числа s, t.
Получить: g(1.2, s)+g(t, s)-g(2s - 1.5t), |g(ln(s, t+1))-g(t, s)|,
где
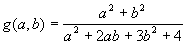
- Даны действительные числа x, y.
Получить: f(x, -2y, 1.17)+f(2.2, x, x-y), tg(f(x+y, xy, y-x)+f(3.1, 1.4, y-sinx)),
где
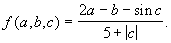
- Даны натуральные числа a, b, c.
Найти НОД(a, b, c), используя формулу:
НОД(a, b, c) = НОД((a, b), c).
- Даны неотрицательные целые числа a, b.
Найти F(a, b), где
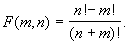 (Определить вспомогательную функцию,
вычисляющую факториал).
(Определить вспомогательную функцию,
вычисляющую факториал).
- Даны две квадратные матрицы A, B 3-го
порядка. Построить таблицу функции y = cx2
+ d при х меняющемся от 0 до 1 с
шагом 0.1, где с = sp(A), d = sp(B). (sp(A)
- след матрицы А - сумма элементов
главной диагонали).
- Даны два натуральных числа a, b.
Найти разность и произведение суммы цифр
этих чисел. Вычисление суммы цифр числа
оформить в виде функции.
- Даны два натуральных числа a, b.
Вычислить
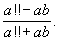
Функция х!! Определяется следующим
образом:
х!! = 1*3*5*...*х, если х нечетно,
х!! = 2*4*6*...*х, если х четно.
- Даны действительные числа a0, a1, a2,
a3. Получить для х = 1, 3, 4 значения р(х+1)
- р(х), где р(у) = a3y3 + a2y2 + a1y +
a0.
- Даны действительные числа a, b, c.
Получить
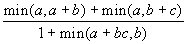 .
.
- Даны действительные числа a, b.
Получить r = max (a, b + a), d = max (ab, a + b), s
= max (r + d2, 3.14).
- Даны натуральные числа a, b, c.
Определить функцию bin (x), переводящую
число х из десятичной системы
счисления в двоичную. Найти двоичное
представление эти чисел.
- Даны действительные числа a, b.
Получить:
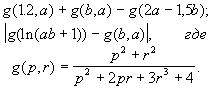
содержание
Задание 2 (процедуры).
- Заданы два вектора х = (x1, x2, x3, x4), y =
(y1, y2, y3, y4). Определить угол a между
векторами x и y по формуле:
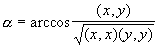 Вычисление скалярного произведения
оформить в виде процедуры.
Вычисление скалярного произведения
оформить в виде процедуры.
- Четыре точки заданы своими координатами
X(x1, x2), Y(y1, y2), Z(z1, z2), P(p1, p2).
Выяснить, какие из них находятся на
максимальном расстоянии друг от друга и
вывести на печать значение этого
расстояния. Вычисление расстояния между
двумя точками оформить в виде процедуры.
- Четыре точки заданы своими координатами
X(x1, x2, x3),
Y(y1, y2, y3),
Z(z1, z2, z3),
T(t1,t2, t3). Выяснить, какие из них находятся на
минимальном расстоянии друг от друга и
вывести на печать значение этого
расстояния. Вычисление расстояния между
двумя точками оформить в виде процедуры.
- Три точки заданы своими координатами X(x1,
x2), Y(y1, y2) и Z(z1, z2). Найти и
напечатать координаты точки, для которой
угол между осью абсцисс и лучом,
соединяющим начало координат с точкой,
минимальный. Вычисления оформить в виде
процедуры.
- Задана окружность (x-a)2 + (y-b)2
= R2 и точки Р(р1, р2), F(f1, f1),
L(l1,l2). Выяснить и напечатать, сколько точек
лежит внутри окружности. Проверку, лежит
ли точка внутри окружности, оформить в
виде процедуры.
- Заданы три матрицы А(первого порядка),
В(второго порядка) и С(третьего
порядка). Выяснить и напечатать, сколько
из них являются симметрическими. (Матрица
называется симметрической, если
транспонированная матрица равна
исходной). Транспонирование матрицы
оформить в виде процедуры.
- Заданы матрицы А и В третьего
порядка. Переменной S присвоить -1,
если максимальный элемент матрицы А
больше максимального элемента матрицы В;
0 если максимальные элементы матрицы
равны; 1, если максимальный элемент
матрицы А меньше максимального
элемента матрицы В. Поиск
максимального элемента оформить в виде
процедуры.
- Заданы два вектора X(x1,x2,x3), Y(y1,y2,y3)
и матрица А третьего порядка. Найти
сумму двух векторов c и d, где
вектор с есть произведение вектора x
на матрицу А, а вектор d -
произведение вектора на матрицу А.
Вычисление произведения вектора на
матрицу оформить в виде процедуры.
- Заданы три матрицы А (третьего
порядка), В (второго порядка) и С (третьего
порядка). Найти максимальное из трех
чисел x, y, z, где x - след
матрицы А, у - след матрицы В, z
- след матрицы С. (Следом матрицы
называется сумма элементов главной
диагонали). Вычисление следа матрицы
оформить в виде процедуры.
- Даны отрезки а, b, c и d. Для
каждой тройки этих отрезков, из которой
можно построить треугольник, вывести на
экран площадь данного треугольника.
Проверку существования треугольника
оформить в виде процедуры.
- Даны длины сторон треугольника a, b,
c. Найти медианы треугольника,
сторонами которого являются медианы
исходного треугольника. Для вычисления
медианы проведенной к стороне а,
использовать формулу
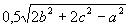 Вычисление медианы оформить в виде
процедуры.
Вычисление медианы оформить в виде
процедуры.
- Даны две матрицы размером 3x3.
Написать программу получения
коммутатора АВ-ВА и антикоммутатора АВ+ВА
этих матриц. Вычисление произведения
матриц оформить в виде процедуры.
- Дана квадратная матрица А. Написать
программу вычисления матрицы Ат*Ат*А*А,
Ат - транспонированная матрица.
Вычисление произведения матриц оформить
в виде процедуры.
- Даны две матрицы А и В. Написать
программу, меняющую местами максимальные
элементы этих матриц. Нахождение
максимального элемента матрицы оформить
в виде процедуры.
- Даны три квадратные матрицы третьего
порядка. Вывести на экран ту из них, норма
которой наименьшая. В качестве нормы
матрицы взять максимум модулей ее
элементов. Нахождение нормы матрицы
оформить в виде процедуры.
содержание
Задание 3.
- Вычислить
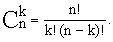 Вычисление факториала числа оформите в
виде подпрограммы.
Вычисление факториала числа оформите в
виде подпрограммы.
- Построить таблицу значений функции
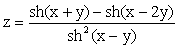 , где x меняется от 1 до 2 с шагом
0,2; y меняется от 2 до 3 с
шагом 0,1. Вычисление гиперболического
синуса
, где x меняется от 1 до 2 с шагом
0,2; y меняется от 2 до 3 с
шагом 0,1. Вычисление гиперболического
синуса 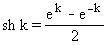 оформить в виде подпрограммы.
оформить в виде подпрограммы.
- Построить таблицу значений функции
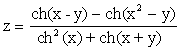 , где x меняется от 3 до 4 с шагом
0,1; y меняется от 2 до 3 с
шагом 0,2. Вычисление гиперболического
косинуса
, где x меняется от 3 до 4 с шагом
0,1; y меняется от 2 до 3 с
шагом 0,2. Вычисление гиперболического
косинуса 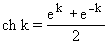 оформить в виде подпрограммы.
оформить в виде подпрограммы.
- Найдите НОД(а, b, c, d) = НОД(НОД(а, b),
НОД(с, d)). Нахождение НОД (наибольшего
общего делителя) двух чисел оформите в
виде подпрограммы.
- Найдите НОК(а, b, c, d) = НОК(НОК(а, b), НОК(с,
d)). Нахождение НОК (наименьшего
общего кратного) двух чисел оформите в
виде подпрограммы.
- Найти все коэффициенты разложения (x+y)n
, т.е.
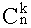 , где k= 0, ..., n. Вычисление
, где k= 0, ..., n. Вычисление 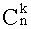 оформите в виде подпрограммы.
оформите в виде подпрограммы.
- Даны длины отрезков a,b,c,d,e. Выяснить,
можно ли построить треугольники со
сторонами {a,b,c}, {b,c,d}, {c,d,e}? Если
да, то найдите площадь соответствующего
треугольника. Проверку на возможность
составления треугольника и вычисление
площади оформите в виде подпрограммы.
- Вычислить
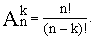 и
и 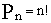 .
Нахождение факториала числа оформите в
виде подпрограммы.
.
Нахождение факториала числа оформите в
виде подпрограммы.
- Найти все пары простых элементов
целочисленного массива A(n) (элементы a
и b взаимно просты, если их наибольший
общий делитель равен 1). Нахождение НОД
двух чисел оформите в виде подпрограммы.
- Отсортировать целочисленный массив по
возрастанию суммы цифр его элементов.
Нахождение суммы цифр числа оформите в
виде подпрограммы.
- Проверить, будут ли числа a, b, c, d
попарно взаимно просты. Числа называются
взаимно простыми, если их наибольший
общий делитель (НОД) равен 1.
Нахождение НОД двух чисел оформить в
виде подпрограммы.
назад содержание
вперед
Волгоградский государственный
педагогический университет
Кафедра алгебры, геометрии и информатики
Май 2082
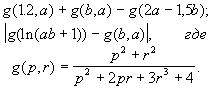
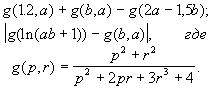
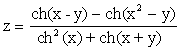 , где x меняется от 3 до 4 с шагом
0,1; y меняется от 2 до 3 с
шагом 0,2. Вычисление гиперболического
косинуса
, где x меняется от 3 до 4 с шагом
0,1; y меняется от 2 до 3 с
шагом 0,2. Вычисление гиперболического
косинуса