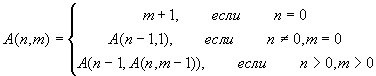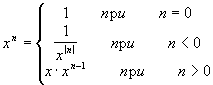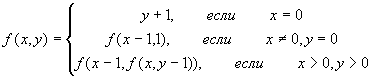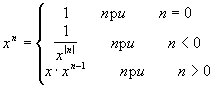1. Даны натуральные числа a, c, m. Получить f(m), 
   где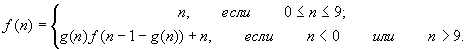
   g(n) - остаток от деления a(n + c) на 10.
2. Даны неотрицательные целые числа n и m. Вычислить функцию Аккермана:
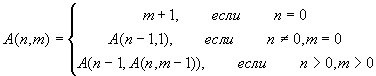
3. Даны два натуральных числа N>1 и M>1. Написать программу нахождения НОД(N,M). Использовать соотношения:
   1) НОД(N, N) = N;
   2) НОД(N, M) = НОД(N-M, M), если N > M;
   3) НОД(N, M) = НОД(N, M-N), если M > N;
4. Написать функцию f(n), которая рекурсивно вычисляет факториал n. Найти сумму a! + b!, где а и b - данные натуральные числа.
5. Даны целые числа p, m и действительные а и b.Найти a^p - b^m. Для вычисления хⁿ использовать рекурсивную функцию, определенную как:
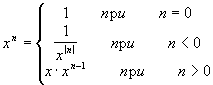
6. Найти С₆³ + С₅³, где 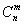- количество сочетаний из n по m. 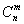рекурсивно вычисляется следующим образом:
   
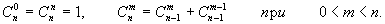
7. Даны натуральные числа p, r, k. Получить f(k), где
   
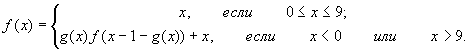
   g(x) - остаток от деления p(x + r) на 10.
8. Даны неотрицательные целые числа x и y. Вычислить функцию:
   
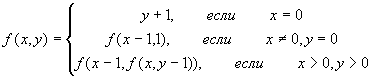
9. Даны два натуральных числа a>1 и b>1. Написать программу нахождения НОД(a, b). Использовать соотношения:
   1) НОД(a, a) = a;
   2) НОД(a, b) = НОД(a-b, b), если a > b;
   3) НОД(a, b) = НОД(a, b-a), если b > a;
10. Написать функцию f(n), которая рекурсивно вычисляет факториал n. Найти сумму t! + k!, где t и k - данные натуральные числа.
11. Даны целые числа i, j и действительные u и v. Найти uⁱ - v^j. Для вычисления хⁿ использовать рекурсивную функцию, определенную как:
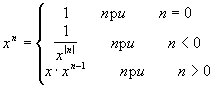
12. Найти С₈⁷ + С₇⁴, где 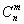- количество сочетаний из n по m. 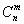рекурсивно вычисляется следующим образом:
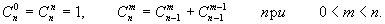
13. Даны натуральные числа a, c, m. Получить f(m), где
    
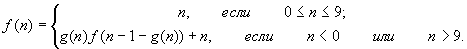
    g(n) - остаток от деления a(n + c) на 10.
14. *Даны две функции f1(x) = ln(x² - 2x + 1), f2(x) = sin(cos x) - 0.7. Найти с точностью eps корни уравнения f1(x) = 0 (на отрезке [1, 3]) и f2(x) = 0 (на отрезке [0.2; 1]), с помощью рекурсивной функции, находящей корень методом деления отрезка пополам.

назад содержание вперед

Волгоградский государственный педагогический университет
Кафедра алгебры, геометрии и информатики
Декабрь 2002